how to find the missing side of a right triangle
Finding a Side in a Right-Angled Triangle
Discover a Side when we know another Side and Angle
We can find an unknown side in a right-angled triangle when nosotros know:
- ane length, and
- one angle (apart from the right angle, that is).
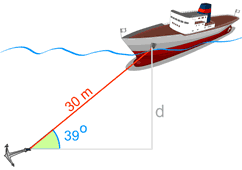
Example: Depth to the Seabed
The ship is anchored on the seabed.
We know:
- the cable length (thirty m), and
- the angle the cable makes with the seabed
So we should be able to find the depth!
But How?
The answer is to employ Sine, Cosine or Tangent!
But Which One?
Which one of Sine, Cosine or Tangent to use?

To observe out which, outset we give names to the sides:
- Adjacent is next (side by side to) to the angle,
- Opposite is reverse the angle,
- and the longest side is the Hypotenuse.
Now, for the side nosotros already know and the side we are trying to observe, we use the get-go letters of their names and the phrase "SOHCAHTOA" to decide which function:
| SOH... | Sine: sin(θ) = Opposite / Hypotenuse | |
| ...CAH... | Cosine: cos(θ) = Adjacent / Hypotenuse | |
| ...TOA | Tangent: tan(θ) = Opposite / Adjacent |
Like this:


Example: Depth to the Seabed (Continued)
Detect the names of the two sides we are working on:
- the side we know is the Hypotenuse
- the side we want to find is Opposite the bending (cheque for yourself that "d" is opposite the angle 39°)
Now use the first messages of those two sides (Opposite and Hypotenuse) and the phrase "SOHCAHTOA" which gives u.s.a. "SOHcahtoa", which tells u.s. we need to use Sine:
Southine: sin(θ) = Opposite / Hypotenuse
At present put in the values we know:
sin(39°) = d / 30
And solve that equation!
But how do we calculate sin(39°) ... ?
 | Use your reckoner. |
sin(39°) = 0.6293...
And then now nosotros have:
0.6293... = d / 30
At present nosotros rearrange it a little bit, and solve:
Outset with: 0.6293... = d / 30
Swap sides: d / 30 = 0.6293...
Multiply both sides by 30: d = 0.6293... x 30
Calculate: d = 18.88 to 2 decimal places
The depth the ballast ring lies beneath the hole is 18.88 m
Stride By Step
These are the four steps to follow:
- Footstep 1 Notice the names of the ii sides we are using, 1 we are trying to find and 1 we already know, out of Contrary, Next and Hypotenuse.
- Step ii Utilise SOHCAHTOA to decide which one of Sine, Cosine or Tangent to employ in this question.
- Step 3 For Sine write downwards Opposite/Hypotenuse, for Cosine write downwards Adjacent/Hypotenuse or for Tangent write downwards Opposite/Adjacent. One of the values is the unknown length.
- Footstep 4 Solve using your computer and your skills with Algebra.
Examples
Allow'due south look at a few more than examples:
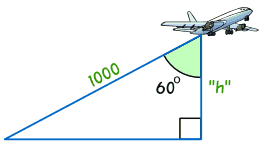
Example: detect the height of the aeroplane.
Nosotros know the distance to the plane is 1000
And the angle is 60°
What is the plane's top?
Conscientious! The 60° angle is at the elevation, so the "h" side is Adjacent to the bending!
- Step one The ii sides we are using are Adjacent (h) and Hypotenuse (1000).
- Step 2 SOHCAHTOA tells usa to apply Cosine.
- Step 3 Put our values into the Cosine equation:
cos 60° = Next / Hypotenuse
= h / g
- Step 4 Solve:
Start with: cos lx° = h/1000
Bandy: h/yard = cos 60°
Calculate cos 60°: h/1000 = 0.5
Multiply both sides past g: h = 0.five 10 thousand
h = 500
The height of the plane = 500 meters
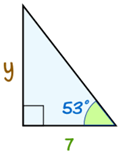
Example: Discover the length of the side y:
- Step 1 The two sides we are using are Opposite (y)
and Adjacent (7).
- Step 2 SOHCAHTOA tells us to use Tangent.
- Footstep 3 Put our values into the tangent part:
tan 53° = Reverse/Next
= y/vii
- Step 4 Solve:
Offset with: tan 53° = y/7
Swap: y/seven = tan 53°
Multiply both sides by 7: y = seven tan 53°
Summate: y = seven x 1.32704...
y = ix.29 (to ii decimal places)
Side y = 9.29
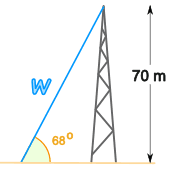
Example: Radio Mast
There is a mast that is seventy meters high.
A wire goes to the top of the mast at an angle of 68°.
How long is the wire?
- Stride 1 The two sides nosotros are using are Opposite (70) and Hypotenuse (w).
- Footstep 2 SOHCAHTOA tells u.s. to use Sine.
- Pace three Write downwardly:
sin 68° = 70/west
- Step four Solve:
The unknown length is on the lesser (the denominator) of the fraction!
Then we need to follow a slightly different approach when solving:
Beginning with: sin 68° = seventy/w
Multiply both sides by w: w × (sin 68°) = 70
Split both sides by "sin 68°": west = seventy / (sin 68°)
Calculate: w = 70 / 0.9271...
due west = 75.5 m (to 1 place)
The length of the wire = 75.5 chiliad
Source: https://www.mathsisfun.com/algebra/trig-finding-side-right-triangle.html
Posted by: dickensevervall.blogspot.com

0 Response to "how to find the missing side of a right triangle"
Post a Comment